De komplekse tal

Kommentarer/spørgsmål?

Lad os vende tilbage til historien om ligninger og tal. Det vil føre for vidt at forklare, hvordan man systematisk indfører tal, som ikke behøver være brøker. Kort sagt laver man dem som uendelige decimaltal, men detaljerne er ret kedelige og lidt besværlige. Så vi vil antage at vi ved hvad (reelle) tal er. Man kan ikke finde et reelt tal, som løser ligningen

x^2 + 1 = 0,

— intet reelt tal ganget med sig selv giver

-1

. Enhver enkel lommerregner vil blinke en fejlmeddelelse, hvis du forsøger at tage kvadratroden til

-1

. Derimod vil et moderne computer algebra system som Maple eller Mathematica formentlig give dig symbolet

I

som output. Hvad er dette

I

Lad os først komme ind på hvor anderledes (og mere spændende) de komplekse tal er med et eksempel fra computergrafik.

Mandelbrotmængden

Geometrisk opholder de komplekse tal sig i to dimensioner, mens de almindelige tal kun bevæger sig på en linje i en dimension.

Man kan benytte de komplekse tal til at generere såkaldte fraktaler som Mandelbrotmængden nedenfor. Mandelbrotmængden er blevet kaldt et af de smukkeste og mest komplicerede objekter i moderne matematik. I næste afsnit ser vi nærmere på addition og multiplikation af komplekse tal. Mandelbrotmængden er frembragt ene og alene ved at iterere multiplikationer og additioner med komplekse tal.

Interaktiv grafik: Du kan udforske et område af Mandelbrotmængden ved at klikke og holde musen nede for at markere et rødt rektangel til at zoome ind på. Det bedste resultat fås ved at markere et kvadrat. Når du zoomer ind på mængden vil du opdage visuel matematisk skønhed og at figuren gentager sig selv.

Kommentarer/spørgsmål?

Regneregler

Mandelbrotmængden fremkommer ved mange iterationer bestående af multiplikationer og additioner med komplekse tal. Vi har brug for at vide hvad komplekse tal er og hvordan man regner med dem.

En specielt vigtig regneregel for reelle tal hedder den distributive lov. Den siger at

x (y + z) = x y + x z

for

x, y, z\in \mathbb{R}

. En anden velkendt regel siger at faktorernes orden er ligegyldig eller at multiplikation er kommutativ dvs

x y = y x

Opgave

Forklar så detaljeret som muligt, hvorfor

(x + y) (z + w) = x z + y z + x w + y w

ved at bruge den distributive lov og kommutativitet for multiplikation.

Lad os antage at vi oven i de reelle tal kaster et opdigtet eller imaginært tal $i$ ind, som har egenskaben at

i^2 = -1.

Hvis

a, b, c, d

er reelle tal og vi antager at

i

adlyder de almindelige regneregler får vi følgende udregning:

\begin{aligned} \color{blue}{(a + b i) (c + d i)} &= (a+ b i) c + (a + b i) d i\\ &= a c + b i c + a d i + b i d i\\ &= a c + b c i + a d i + b d i^2\\ &= a c + b c i + a d i - b d\\ &= \color{blue}{(a c - b d) + (a d + b c) i} \end{aligned}

Dvs to tal på formen $x + y i$ , hvor $x$ og $y$ er reelle tal, ganger sammen til et tal af samme standard form.

Kommentarer/spørgsmål?

Faktisk kan man vise at, når man definerer multiplikation som ovenfor og addition som

(a + b i) + (c + d i) = (a + c) + (b + d)i,

så får man en mængde af nye tal, som opfylder alle velkendte regneregler for reelle tal, som f.eks.

\begin{aligned} x (y z) &= (x y) z\\ x( y + z) &= x y + x z\\ x y & = y x\\ 1 x &= x \end{aligned}

Opgave

Den ukronede konge blandt regnereglerne er reglen

x (y z) = (x y) z

, som kaldes den associative lov. Uformelt siger den at vi selv kan vælge hvordan vi udregner et produkt

x y z

: Det gør ikke nogen forskel om vi først ganger

x

sammen med

y

og så ganger

z

på eller om vi først ganger

y

sammen med

z

og så ganger

x

på. Det giver det samme resultat. Hvis vi ikke havde den associative lov ville (den aritmetiske) verden være kaotisk.

Faktisk kan vi allerede nu se at den associative lov gælder for vores nye tal af formen $a + b i$ : Lad $x = a + b i, y = c + d i$ og $z = e + f i$ , hvor $a, b, c, d, e, f$ er reelle tal.

Udregn $u = y z$ ved at sætte ind i formlen.
Udregn $v = x y$ ved at sætte ind i formlen.
Udregn $x u$ og $v z$ ved at sætte ind i formlen.
Overbevis dig nu om at $x (y z) = (x y) z$ dvs at $x u = v z$ .

Hvorfor benyttes notationen $i$ for $\sqrt{-1}$ ? Begrundelsen er historisk og daterer sig tilbage til $1500$ -tallet, hvor den italienske matematiker Cardano havde behov for at regne med opdigtede eller imaginære tal for at finde en formel til løsning af tredjegradsligninger. Det komplekse tal $i$ kaldes for den imaginære enhed.

De komplekse tal er mængden

\mathbb{C} = \{x + y i \mid x, y\in \mathbb{R}\},

hvor multiplikation er givet som

(a + b i) (c + d i) = (a c - b d) + (a d + b c) i

og addition som

(a + b i) + (c + d i) = (a + c) + (b + d)i.

For et komplekst tal

z = x + i y

defineres

Realdelen som $\mathrm{Re}(z) = x$
Imaginærdelen som $\mathrm{Im}(z) = y.$
Det komplekst konjugerede tal $\overline{z} = x - i y$

To komplekse tal er identiske hvis og kun hvis deres real- og imaginærdele er ens.

Ved hjælp af formlen for multiplikation af komplekse tal ses for $z = c + d i$ , at

z \overline{z} = (c + d i) (c - d i) = c^2 + d^2

ved indsættelse af

a = c

b = d

c=c

d = -d

. Denne observation gør at vi kan udlede følgende divisionsformel:

\begin{aligned} \color{blue}{\frac{a + b i}{c + d i}}&= \frac{(c - d i)(a + b i)}{(c - d i)(c + d i)}\\ &= \frac{(a c + b d) + (a d - b c)i} {c^2 + d^2}\\ &= \color{blue}{\frac{a c + b d}{c^2 + d^2} + \frac{a d - b c}{c^2 + d^2} i}. \end{aligned}

Divisionen af to komplekse tal giver altså igen et komplekst tal. Vi antager at tælleren $c + d i$ ikke er lig $0$ dvs $c$ og $d$ ikke begge er $0$ eller ækvivalent hermed at $c^2 + d^2 \neq 0$ .

Kommentarer/spørgsmål?

En meget vigtig egenskab er at hvis $a + b i\neq 0$ , så findes $c + d i$ så $(a+ b i) (c + d i) = 1$ . Vi ved godt denne regel er korrekt for de reelle tal dvs, hvis $x \neq 0$ så findes et reelt tal $y$ så $x y = 1$ . Her kan vi bare sætte $y = 1/x$ . På samme måde kan vi sætte $c + d i = 1/(a + b i)$ .

Opgave

Find en formel for

1/(a + b i)

, hvor

a

b

ikke begge er

0

Opgave

Find $z\in \mathbb{C}$ , som opfylder at $z (1 + i) = (1 + 2 i)$ .
Find $z_1, z_2\in \mathbb{C}$ , som opfylder $\begin{aligned} (1-2 i) z_1 + z_2 &= 8 + 4 i\\ z_1 + i z_2 &= -3 + 5 i \end{aligned}$

Geometrisk fortolkning og polær form

Den geometriske fortolkning af de komplekse tal blev først introduceret af den danske matematiker Caspar Wessel (1745-1818) i 1797.

Det forekommer ret naturligt at opfatte et komplekst tal $z = x + i y$ , som punktet $(x, y)$ i et koordinatsystem.

Med dette geometriske billede ligger det lige for at indføre følgende definitioner.

Lad

z = x + i y

være et komplekst tal. Længden af vektoren

(x, y)

kaldes modulus for

z

og betegnes

\left\vert z \right\vert

. Vinklen som

(x, y)

danner med

x

-aksen kaldes argumentet for

z

og defineres som en vinkel i intervallet

[0, 2\pi)

. For et reelt tal

x\in \mathbb{R}

definerer vi det komplekse tal

e^{i x} = \cos(x) + i \sin(x). \tag{2.1}

Læg mærke til at hvis $\theta$ er argumentet for det komplekse tal $z$ , så er

\frac{z}{\left\vert z \right\vert} = e^{i \theta}. \tag{2.2}

Det er fordi at

z/\left\vert z \right\vert

præcis svarer til vektoren

(x, y)

ganget med dens reciprokke længde. Denne vektor er en enhedsvektor, som danner vinklen

\theta

med

x

-aksen. Dvs den svarer præcis til det komplekse tal

e^{i\theta}

Ligningen (2.2) giver den smukke geometriske repræsentation

z = \left\vert z \right\vert e^{i\theta} \tag{2.3}

af det komplekse tal

z

. Fremstillingen (2.3) kaldes for den polære form af

z

Denne repræsentation fortjener at blive kaldt smuk, fordi den afspejler sig mirakuløst i multiplikationen af komplekse tal: Lad $z_1$ og $z_2$ være to komplekse tal med argumenter hhv $\theta_1$ og $\theta_2$ . Så er

z_1 z_2 = \left\vert z_1 \right\vert e^{i\theta_1} \left\vert z_2 \right\vert e^{i \theta_2} = \left\vert z_1 \right\vert \left\vert z_2 \right\vert e^{i\theta_1} e^{i \theta_2} =\left\vert z_1 \right\vert \left\vert z_2 \right\vert e^{i(\theta_1+ \theta_2)}. \tag{2.4}

Med ord har vi gjort rede for at

Man multiplicerer to komplekse tal ved at multiplicere deres længder og addere deres argumenter.

Det sidste lighedstegn i (2.4) har vi rent faktisk ikke vist og det er da også et af hovedresultaterne:

For to tal

x, y\in \mathbb{R}

gælder formlen

e^{i x} e^{i y} = e^{i (x + y)}.

Bevis

Vi bruger multiplikation af komplekse tal og ganger

e^{i x} = \cos(x) + i \sin(x)

e^{i y} = \cos(y) + i\sin(y)

sammen:

\begin{aligned} &e^{i x} e^{i y} = (\cos(x) + i\sin(x)) (\cos(y) + i\sin(y)) =\\ &\cos(x) \cos(y) - \sin(x) \sin(y) + i (\cos(x) \sin(y) + \sin(x) \cos(y))=\\ &\cos(x + y) + i \sin(x + y) = e^{i (x+y)}. \end{aligned}

Her forekommer miraklet i næstsidste og sidste linje ovenfor. Multiplikationen af komplekse tal indeholder additionsformlerne:

\begin{aligned} \cos(x + y) &= \cos(x) \cos(y) - \sin(x) \sin(y)\\ \sin(x + y) &= \cos(x) \sin(y) + \sin(x) \cos(y) \end{aligned}

for cosinus og sinus.

Læg iøvrigt mærke til verdens smukkeste formel:

e^{i \pi} = -1.

Formlen kombinerer på minimal vis fire af de allervigtigste konstanter i matematikken: $e, i, \pi$ og $1$ og følger af definitionen i (2.1).

Kommentarer/spørgsmål?

De Moivres formel

Abraham de Moivre var en fransk matematiker, som udover at beskæftige sig med sandsynlighedsteori også fik sit navn udødeliggjort gennem De Moivres formel. Denne formel siger i al sin enkelhed at der for et naturligt tal $n$ og et reelt tal $x$ gælder

(\cos(x) + i \sin(x))^n = \cos(n x) + i \sin (n x). \tag{2.5}

Det er ikke svært at bevise formlen via sætningen ovenfor, som medfører at

(\cos(x) + i \sin(x))^n = (e^{i x})^n = e^{i n x} = \cos(n x) + i \sin( n x).

Ikke desto mindre er (2.5) et mirakel, som markerer den stærke forbindelse mellem komplekse tal og trigonometriske funktioner. For eksempel kan man benytte De Moivres formel til at udlede formler som

\cos(3 x) = 4 \cos(x)^3 - 3 \cos(x). \tag{2.6}

Kommentarer/spørgsmål?

Quiz

Hvad er

\cos(2 x)

2 \sin(x) \cos(x) + 1

2 \cos(x)^2 - 1

Ingen af de foregående svarmuligheder.

Opgave

Find en stamfunktion til

\cos(x)^3

Andengradsligningen og højeregradsligninger

Lad os rette opmærksomheden mod ligningen

z^n = 1, \tag{2.7}

hvor

n

er et naturligt tal. Hvis vi kun begrænser os til de reelle tal, har (2.7) højst to løsninger (feks for

n=2

) og nogle gange kun en (feks for

n=3

). I de komplekse tals domæne har vi to dimensioner og kan boltre os både lodret og vandret. En løsning

z

til (2.7) bliver nødt til at have modulus

1

dvs

z = e^{i\varphi}

med

\varphi\in [0, 2\pi)

. Da

z^n = e^{i n \varphi} = \cos(n \varphi) + i \sin (n \varphi) = 1

har vi altså

m 2 \pi = n \varphi

for et helt tal

m\in \mathbb{Z}

. Hvis

\varphi

er argumentet for

z

har vi altså kun mulighederne

m = 0, 1, \ldots, n-1

Dermed kan alle løsninger til (2.7) skrives som passende potenser af $\epsilon_n = e^{i 2 \pi/n}$ :

\epsilon_n^m = e^{m \frac{2\pi i}{n}},

hvor

m = 0, 1, \ldots, n-1

. Vi har faktisk bevist at (2.7) altid har

n

forskellige løsninger over de komplekse tal.

Eksempel

Lad os som eksempel tage ligningen $z^3 = 1$ . Den har løsningerne, som fremkommer ved at tredele enhedscirklen;

i $\mathbb{C}$ dvs

\begin{aligned} z_0 &= 1\\ z_1 &= e^{i \frac{2 \pi}{3}} = -\frac{1}{2} + \frac{\sqrt{3}}{2} i\\ z_2 &= e^{i \frac{4 \pi}{3}} = -\frac{1}{2} - \frac{\sqrt{3}}{2} i \end{aligned}

Quiz

Lad

z

være en løsning til

z^8 = 1

. Hvilke muligheder er der for

z

|z| = 2

z = i

Argumentet for

z

\pi/8

z = \frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2}.

Lad

n

være et naturligt tal og

a = r e^{i \theta}

et komplekst tal med modulus

r\neq 0

og argument

\theta

. Så har ligningen

z^n = a \tag{2.8}

løsningen

\omega = \sqrt[n]{r} e^{i \frac{\theta}{n}}.

Ligningen (2.8) har

n

forskellige løsninger og de er

\omega, \omega \epsilon_n , \ldots, \omega \epsilon_n^{n-1},

hvor

\epsilon_n = e^{i \frac{2\pi}{n}}

Bevis

At opløfte et komplekst tal til

n

-te potens svarer til at opløfte dets modulus til

n

-te og gange dets argument med

n

. Derfor er

\omega^n = r e^{i\theta}

og dermed en løsning til

z^n = a

. Antag nu at

u^n = a

. Så vil

\frac{u^n}{\omega^n} = \left(\frac{u}{\omega}\right)^n = 1.

Dermed vil

\frac{u}{\omega}

være en løsning til

z^n = 1

, hvorfor

u = \omega \epsilon_n^m

for et eller andet

m

blandt

0, \ldots, n-1

Den gode gamle andengradsligning

Her støder vi på det verdensberømte trick (completing the square):

a z^2 + b z + c = a\left(z + \frac{b}{2a}\right)^2 - \frac{b^2}{4 a} + c.

Ved en lettere omskrivning ses at løsninger til andengradsligningen

a z^2 + b z + c = 0

opfylder

\left(z + \frac{b}{2 a}\right)^2 = \frac{b^2 - 4 a c}{4 a^2}.

Det giver så den klassiske formel

z = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a},

som giver rigtig god mening også for komplekse tal

a, b, c

. Vi har nemlig set i sætningen ovenfor at ligningen

w^2 = b^2 - 4 a c \tag{2.9}

altid kan løses dvs andengradsligninger over de komplekse tal har altid løsninger! Det gør ikke nogen forskel hvilken af de to modsat rettede løsninger

w

vi vælger i (2.9) som

\sqrt{b^2 - 4 a c}

. Den klassiske formel gælder stadig pga

\pm

Opgave

Vis at

\epsilon_3 = e^{i \frac{2\pi}{3}}

er en løsning til andengradsligningen

z^2 + z + 1 = 0.

Benyt dette til at finde et udtryk for sinus til

120

grader (

2\pi/3

) ved hjælp af løsningsformlen for andengradsligningen.

Algebraens fundamentalsætning

Vi så ovenfor at andengradsligninger altid har løsninger i de komplekse tal. Det helt enestående er at dette resultat også gælder for $n$ -te grads ligninger dvs ligninger af formen

a_n z^n + a_{n-1} z^{n-1} + \cdots + a_1 z + a_0 = 0,

hvor

a_n, \ldots, a_0\in\mathbb{C}

a_n\neq 0

. Vi har blot vist det for

n=2

, men det gælder for alle

n = 1, 2, 3, \ldots

Denne perle kaldes for algebraens fundamentalsætning. Det er spændende at læse om historien bag denne sætning.

Der er endnu ikke opdaget et algebraisk bevis for sætningen a la det vi lavede for $n=2$ .

Om komplekse tal og periodiske fænomener

Cosinus og sinus er rasende interessante funktioner. De er matematikkens fremmeste våben i beskrivelsen af periodiske fænomener som feks planetbaner og bølgebevægelser. De bliver endnu mere anvendelige, når man betragter dem ved hjælp af den komplekse eksponentialfunktion $e^{i x}$ .

En periodisk funktion $f(t)$ er en funktion, som gentager sig selv efter et bestemt tidsrum $T$ dvs $f(t) = f(t + T)$ . For eksempel er både sinus og cosinus periodiske funktioner med periode $T = 2\pi$ .

Uden at afsløre den fulde sandhed kan jeg her skrive at man normalt kigger på cosinus og sinus funktioner på formen

A \cos(N x)\qquad \mathrm{og} \qquad A \sin(N x), \tag{2.10}

hvor

A

er et tal, som angiver højden (amplituden) af bølgerne og

N

er et tal, som beskriver antal bølger per tidsenhed (frekvensen). Cosinus og sinusfunktionerne i (2.10) samles under et i funktionerne

A e^{i N x}

Disse funktioner er byggeklodser for naturligt forekommende periodiske fænomener.

Feks er den periodiske funktion $\cos(x)^3$ :

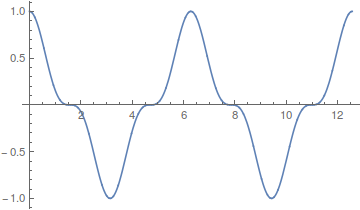
sum af de to periodiske funktioner $\frac{1}{4} \cos(3 x)$ og $\frac{3}{4} \cos(x)$ :

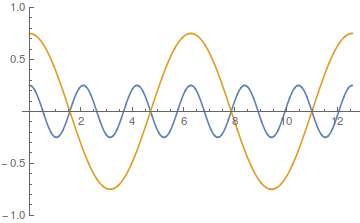
Dette kan aflæses af formlen i (2.6), som vi netop fik ved hjælp af

(e^{i x})^3 = e^{i (3 x)}.

Vi vender tilbage til opløsningen af et signal (en periodisk funktion) i komponenterne

A e^{i N x}

senere. Faktisk er det sådan man digitaliserer feks musik.

Opgaver

Quizopgave

Hvad gælder om

z=(1-i)(2+i)

z

svarer til at gange

2+i

med

\sqrt{2}

og derefter gange med

e^{i \pi/4}

z=2-i

z = 3-i

z

svarer til at gange

2+i

med

\sqrt{2}

og derefter med

e^{i 7\pi /4}

Kommentarer/spørgsmål?

Gør rede for at

e^{i x} e^{-i x} = 1

, hvis

x\in \mathbb{R}

. Hvad er den polære form for

z^{-1} = 1/z

, hvis

z

har polær form

z = r e^{i \theta}?

Hvad med den polære form for det konjugerede komplekse tal

\overline{z}

Kommentarer/spørgsmål?

Quizopgave

Hvad gælder om

z=(2+i)/(1-i)

z

svarer til at dividere

2+i

med

\sqrt{2}

og derefter gange med

e^{i \pi/4}

2 z=1+3 i

z = -1 + 3 i

z

svarer til at gange

2+i

med

\sqrt{2}

og derefter med

e^{- i \pi /4}

Kommentarer/spørgsmål?

Løs andengradsligningen

z^2 -(3+2i)z + (1 + 3i) = 0.

Kommentarer/spørgsmål?

Opskriv samtlige komplekse tal

z

, som løser ligningen

z^6 = 64.

Hvilke af disse løsninger er reelle tal?

Kommentarer/spørgsmål?

Find reelle tal

A

f

så at

\cos(t) + \sin(t) = A \cos(t + f)

for alle

t

(

A

kaldes amplituden og

f

faseforskydningen af "signalet" på venstresiden).

Vink

Opfat venstresiden som realdelen af

e^{i t} - i e^{i t}

og højresiden som realdelen af

A e^{i (t + f)}.

og regn med komplekse tal!

Kommentarer/spørgsmål?

Generaliser den foregående opgave til at finde

C

f

ud fra

\omega, A

B

så

A \cos(\omega t) + B \sin(\omega t) = C \cos(\omega t + f).

Kommentarer/spørgsmål?