1A partly topological introduction

The brief version is that an algebraic curve, or rather a plane algebraic curve, is the zero locus of a polynomial in two variables. To define this in more precision, let $k$ be a field. Then the zero locus of $F\in k[x, y]$ is

$V(F) = \{(a, b)\in k^2 \mid F(a, b) = 0\}$

For $k = \mathbb{R}$ and $F = x^2 + y^2 - 1$ we get the well known unit circle.

But we may also have more complicated curves like

given by $V(F)$ , where $F = x^3 + y^3 - 3 x y$ . The unit circle has the (well?) known parametrization

$\begin{aligned} x &= \frac{2 t}{1 + t^2}\\ y &= \frac{1 - t^2}{1 + t^2}. \end{aligned}\tag{1.1}$ Such a parametrization (with rational functions) always misses a finite number of points on the curve. If you include transcendental functions, you can get all the points (here with $t$ only running through a closed and bounded interval!) with the parametrization

$\begin{aligned} x &= \cos(t)\\ y &= \sin(t). \end{aligned}\tag{1.2}$ Can you find a similar parametrization as in (1.1) for the (famous) curveThis curve is called the folium of Descartes in Figure (1.3)? Here the rules of the game are: find rational functions $p(t), q(t)\in \mathbb{R}(t)$ , such that

$F(p(t), q(t)) = 0,$ where $F = x^3 + y^3 - 3 x y$ .

Prove that $x^2 + y^2 - 1$ and $x^3 + y^3 - 3 x y$ are irreducible polynomials in $\mathbb{R}[x, y]$ .

Challenge

Prove that (the Fermat curve)

$x^n + y^n = 1$ does not have solutions in the field $k(t)$ of rational functions in the variable $t$ for $n>2$ . Here $k$ is any field.

Studying mathematics a century ago, you would probably in a flash be able to spot that

$\int \sqrt{x^2 - 5 x + 6}\, d x = \left(\frac{x}{2}-\frac{5}{4}\right) \sqrt{x^2-5 x+6}-\frac{1}{8} \log \left(-2 \sqrt{x^2-5 x+6}-2 x+5\right). \tag{1.3}$

You can see that Sage says about this indefinite integral by evaluating the window below.

The algebraic curve $V(F)$ given by $F = y^2 - x^2 + 5 x - 6$ is parametrized by

$\begin{aligned} x &= \frac{2 t^2 - 3}{t^2-1}\\ y &= \frac{t}{t^2-1}. \end{aligned}$ How does this help you in computing an antiderivative of $\sqrt{x^2 - 5 x + 6}$ ? Carry out the computation using a computer algebra system and verify that you get an antiderivative.

The antiderivative

$\int \sqrt{x^3 + 1}\, d x$ is a different story, partly because it is impossible to find a rational parametrization of the algebraic curve $V(y^2 - x^3 - 1)$ .

Classically (and astronomically!) ellipses are extremely interesting. An ellipse is an algebraic curve of the form $V(F)$ for

$F = \left(\frac{x}{A}\right)^2 + \left(\frac{y}{B}\right)^2 - 1,$ where $A, B > 0$ . It has the transcendental parametrization

$\begin{aligned} x &= A \cos(t)\\ y &= B \sin(t). \end{aligned}$

Kepler approximated the circumference using the formula $\pi (A + B)$ . If you want to compute the circumference precisely, you run into a bit of trouble when trying find the antiderivative below

$4 \int_0^{\pi/2} \sqrt{A^2 \sin^2(t) + B^2 \cos^2(t)}\, dt = 4 B \int_0^{\pi/2} \sqrt{1 - \lambda \sin^2(t)}\, d t,$ where $\lambda = 1 - \frac{A^2}{B^2}$ .

1.1 A few words about rational functions

The subset $V(F) \subseteq \R^2$ could be called an algebraic set. What are algebraic functions? To start with let us define rational functions

$\mathbb{R}(x, y) = \left\{\frac{f(x, y)}{g(x, y)}\, \middle|\, f, g,\in \mathbb{R}[x, y], g\neq 0\right\}. \tag{1.4}$ There are many representatives for a rational function $q\in \mathbb{R}(x, y)$ when defined as in (1.4). Just take a look at the example below for the rational functions $\mathbb{R}(x)$ in just one variable.

In an exercise in my first year course Introduction to mathematics and optimization, I asked students to analyze the behavior of the rational function

$q(x) = \frac{x^2 - 3 x + 2}{x^2-4 x + 3}$ close to $x=1$ . Clearly $q(x)$ is not defined for $x = 1$ , but it turns out that everything works out, since

$q(x) = \frac{(x-1)(x-2)} {(x-1)(x-3)} = \frac{x-2}{x-3}.$ It looks like $q(x)$ is not defined for $x = 1$ , but it is! It may be defined in one representation, but not in another.

A rational function $q\in \mathbb{R}(x, y)$ can be restricted to an algebraic curve $V(F)$ and we may evaluate $q$ given by a representative $q = f/g$ in a point $P\in V(F)$ provided that $g(P)\neq 0$ (if $g$ is in the principal ideal $(F)$ , we are doomed). Here the representative for the rational function is even more deceiving than in Example 1.8.

The unit circle $S^1$ is given by $V(F)$ , where $F = x^2 + y^2 - 1$ . The rational function

$t = \frac{y-1}{x}\in \mathbb{R}(x, y)$ restricts to give a function on $V(F)$ . Does this rational function haves poles in $(0, 1)$ and $(0, -1)$ ? The funny thing is that when we restrict $t$ to $V(F)$ , then

$t = \frac{y-1}{x} = -\frac{x}{y+1}$ as rational functions on $V(F)$ . Therefore $t$ is well defined at $(0, 1)$ with value $0$ . The above identity leads to the system

$\begin{aligned} - t x + y &= 1\\ - x - t y &= t \end{aligned}$ of linear equations over the subfield $\mathbb{R}(t) \subseteq \mathbb{R}(x, y)$ with solutions

$\begin{aligned} x &= \frac{-2 t}{1 + t^2}\\ y &= \frac{1 - t^2}{1 + t^2}. \end{aligned}\tag{1.5}$ If you look closer, we have actually proved algebraically that the field of rational functions (properly defined) on $S^1$ is isomorphic to $\mathbb{R}(t)$ .

1.2 Topology

Recall that a topological space is a set $X$ with a topology. A topology is a subset $\tau \subset 2^X$ of socalled open subsets, such that

$\emptyset\in \tau$
$X\in \tau$
$\bigcup_{i\in I} U_i\in \tau$ if $U_i\in \tau$ for $i\in I$ .
$U_1 \cap \cdots \cap U_n\in \tau$ if $U_1, \dots, U_n\in \tau$ .

This definition is so extremely basic and surprising. Even though topology was existing in the $19$ th century, the definition of a topological space is from 1914.

Suppose that $X$ is a metric space with metric $d$ . What is the natural topology associated with $d$ ?

A map

$f : X \rightarrow Y$ between topological spaces with topologies $\tau_X\subseteq 2^X$ and $\tau_Y\subseteq 2^Y$ is called continuous if $f^{-1}(U)\in \tau_X$ for $U\in \tau_Y$ .

If a continuous map is bijective, then its inverse map is not necessarily continuous. If its inverse map is continuous, then the bijection is called a homeomorphism.

Give an example of a continuous bijective map whose inverse map is not continuous.

A closed subset of a topological space $X$ is the complement of an open subset. Therefore the axioms for a topological space might as well be given for the set $\varphi = \{X\setminus U \mid U\in \tau\}\subset 2^X$ of closed subsets:

$\emptyset\in \varphi$
$X\in \varphi$
$\bigcap_{i\in I} F_i\in \varphi$ if $F_i\in \varphi$ for $i\in I$ .
$F_1 \cup \cdots \cup F_n\in \varphi$ if $F_1, \dots, F_n\in \varphi$ .

1.2.1 Induced topology

A subset $Z \subset X$ of a topological space $X$ carries the socalled induced topology, which is defined by

$\{Z \cap U \mid U\in \tau_X\}.$

The closure $\overline{Y}$ of a subset $Y\subset X$ is the smallest closed subset containing $Y$ . It is the intersection of the closed subsets containing $Y$ . If

$X = U_1 \cup \cdots \cup U_n$

is an open cover, then

$\overline{Y} = \overline{Y\cap U_1} \cup \cdots \cup \overline{Y\cap U_n},$

where $\overline{Y\cap U_i}\subseteq U_i$ denotes closure in the induced topology.

1.2.2 Quotient topology

Let $\sim$ be an equivalence relation on a topological space $X$ . The equivalence class containing $a\in X$ is defined by

$[a] = \{x\in X \mid x \sim a\} \subset X.$ Recall that $[a] \neq [b]\implies [a] \cap [b] = \emptyset$ . The set of equivalence classes is

$X/_\sim = \{[a] \mid a\in X\}.$ There is a natural topology on $X/_\sim$ , such that $U\subset X/_\sim$ is an open subset if and only if $\pi^{-1}(U)$ is open in $X$ . Here

$\pi: X \rightarrow X/_\sim$ is the canonical map given by $\pi(x) = [x]$ . This topology on $X/_\sim$ is called the quotient topology on $X$ .

Prove that the quotient topology is a topology.

If $G$ is a topological group (group operations are continuous maps) and $H$ a subgroup, then $G/H$ is naturally a topological space. Furthermore, $\pi: G\rightarrow G/H$ is an open map i.e., $\pi(U)\subset G/H$ is an open subset of $G/H$ . Recall that

$G/H = \{ g H \mid g\in H\}\quad\text{and}\quad \pi(g) = gH.$ Therefore $\pi^{-1}(\pi(U)) = \bigcup_{h\in H} U h$ is an open subset as a union of open subsets in $G$ .

Consider $X = [0, 1]$ and $\sim$ with $0\sim 1$ and $x\sim x$ for $x\in X$ . Then

$\pi\left([0, \frac{1}{2})\right) \subset X/\sim$ is not an open subset.

1.2.3 Compactness

A topological space $X$ is called compact if every open cover has a finite subcover i.e.,

$X = \bigcup_{i\in I} U_i \quad\implies \quad X = \bigcup_{j\in I_1} U_i.$ where $U_i$ is an open subset and $I_1\subset I$ is a finite subset. This is also a very cool and surprising definition. The result below is called the Heine-Borel theorem.

A subset of a euclidean space $\mathbb{R}^n$ with the usual metric (and topology) is compact if and only if it is closed and bounded.

Give an example of a metric space, where closed and bounded subsets are not necessarily compact.

Hint

Consider $X = [0, 2]\cap \mathbb{Q}\subset \mathbb{R}$ .

Hint

Along with the open covering given by

$U_n = \{x\in X \mid |x^2 - 2| > 1/n\}$ for $n = 1, 2, \dots$ .

The unit circle $V(x^2 + y^2 - 1)\subseteq \mathbb{R}^2$ is a compact topological space.

We also recall the following result, the proof of which is surprisingly straight forward. Notice how clean the statement is. No epsilons, no deltas. Just pure set theory.

Let $f: X\rightarrow Y$ be a continuous map between topological spaces. Then $f(X)$ is compact if $X$ is compact.

A consequence of the above result is that a continuous function $f:X\rightarrow \mathbb{R}$ on a compact topological space attains its supremum and infimum.

1.2.4 Hausdorff

A topological space $X$ is called Hausdorff if for every set of distinct point $x, y\in X$ there exists open subsets $U, V\in X$ , such that

$x\in U, y\in V\qquad\text{and} \qquad U\cap V = \emptyset.$ This notion has a nice interplay with compactness:

A compact subset of a Hausdorff topological space is closed.

Proving the above proposition also amounts to playing around with the abstract concepts. Once you get down to it, the proof is surprisingly short.

From Theorem 1.19 it follows that

Let $f: X\rightarrow Y$ be a continuous map, where $X$ is compact and $Y$ is Hausdorff. Then $f$ is closed i.e., $f(Z)\subset Y$ is a closed subset if $Z\subset X$ is a closed subset.

To elucidate the result above: let $\pi: \mathbb{R}^2 \rightarrow \mathbb{R}$ denote the projection on the first coordinate. Can you give an example of a closed subset $Z\subset \mathbb{R}^2$ , such that $\pi(Z)\subset \mathbb{R}$ is not closed?

Give a precise proof that the topological spaces

$\mathbb{R}/2\pi \mathbb{Z} \qquad \text{and} \qquad S^1 = \{z\in \mathbb{C} \mid |z| = 1 \}$ are homeomorphic.

1.2.5 Product topology

We will briefly introduce the product topology. To simplify, we do this only for the product $X\times Y$ of two topological spaces $X$ and $Y$ . The product topology on $X\times Y$ is defined as the smallest topology containing $X\times V$ and $U\times Y$ , where $U$ is an open subset of $X$ and $V$ is an open subset of $Y$ . So a subset $W\subset X\times Y$ is open if and only if for every $(x, y)\in W$ , there exists open subsets $U\subset X$ and $V\subset Y$ , such that $(x, y)\in U\times V$ and $U\times V\subset W$ .

You should check that a topological space $X$ is Hausdorff if and only if the diagonal $\Delta_X \subset X\times X$ is closed in the product topology.

1.2.6 Connectedness

A topological space $X$ is connected if it is not the disjoint union of two non-empty subsets. If $f: X \rightarrow Y$ is a continuous map, then $f(X)$ is connected if $X$ is connected.

1.2.7 Irreducibility

This is a notion you may not have seen before.

A topological space is called irreducible if it is not the union of two proper closed subsets.

What are the irreducible subsets (as topological spaces) of $\mathbb{R}$ ?

1.2.8 Complex vector spaces

The set $\mathbb{C}^n$ is a normed vector space over $\mathbb{C}$ with

$||(z_1, \dots, z_n)|| = \sqrt{z_1 \overline{z}_1 + \dots + z_n \overline{z}_n}.$

It is perfectly ok to view $\mathbb{C}^n$ as $\mathbb{R}^{2n}$ as a topological space. In fact, if $z_1 = x + i y$ and $z_2 = u + i v$ , then we have in $\mathbb{C}^2$ that

$||(z_1, z_2) || = \sqrt{x^2 + y^2 + u^2 + v^2}.$

Prove that $V(x^2 + y^2 - 1)\subset \mathbb{C}^2$ is not a compact topological space.

Let $F(x, y)\in \mathbb{C}[x, y]$ be a non-constant polynomial in two variables. Prove that $V(F)\subset \mathbb{C}^2$ is not a compact topological space.

1.3 Compactification

1.3.1 The real line

The solution in (1.5) gives us a bijective continuous map (a homeomorphism!) $\varphi: \mathbb{R}\rightarrow S^1\setminus\{P\}$ given by

$\varphi(x, y) = \left(\frac{2 t}{t^2 + 1}, \frac{t^2- 1}{t^2 + 1}\right), \tag{1.6}$ where $P = (0, 1)$ . I find it intriguing that an infinitely large set of numbers, such as $\mathbb{R}$ can be curled into the compact space $S^1$ except for one point. This construction is an example of a socalled compactification. It turns out that every algebraic curve has one.

Prove precisely that $\varphi$ in (1.6) is a homeomorphism.

1.3.2 The famous Riemann sphere

In section 1.3.1 we embedded $\mathbb{R}$ in the compact topological space $S^1$ by merely adding one point to $\mathbb{R}$ ! It turns out we can do the same with $\mathbb{C}$ . Topologically the compactification is the unit sphere in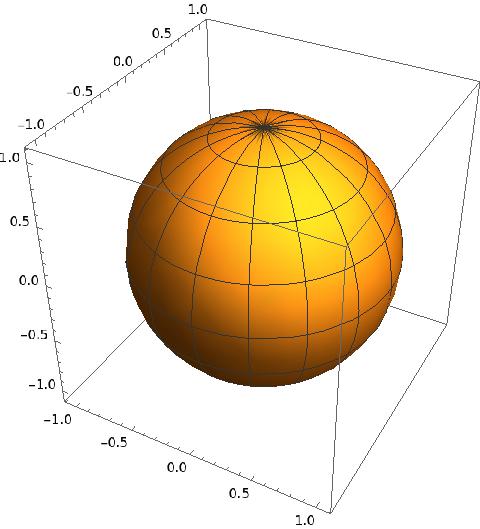 $\mathbb{R}^3$ i.e.,

$S^2 = \{(x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1\}.$

We define a map (the inverse of stereographical projection) $\Phi: \mathbb{C}\rightarrow S^2\setminus\{\infty\}$ , where $\infty$ is the north pole $(0, 0, 1)$ .

To $z = x + i y$ we associate

$\Phi(z) =\left(\frac{2 x}{x^2 + y^2 + 1}, \frac{2 y}{x^2 + y^2 + 1}, \frac{x^2 + y^2 - 1}{x^2 + y^2 + 1}\right)$ Notice that

$\Phi^{-1}(x, y, z) = \frac{x}{1-z} + i \frac{y}{1-z}.$

Let $\sigma:S^2\setminus\{S\}\rightarrow \mathbb{C}$ be stereographic projection from the south pole i.e.,

$\sigma(x, y, z) = \frac{x}{1+z} + i \frac{y}{1+z}.$ Let $\varphi = \sigma \circ \Phi$ . Prove that

$\varphi(z) = \frac{1}{\overline{z}}$ and that $\varphi$ is not holomorphic. Can you make a small adjustment $\sigma'$ to $\sigma$ so that $\sigma'\circ \Phi$ becomes holomorphic? With this adjustment the Riemann sphere becomes a Riemann surface!

If you have a sequence $z_1, z_2, \dots$ of complex numbers tending to infinity, then they actually converge (!) on the Riemann sphere to $\infty$ - the north pole. Riemann defined $\overline{\mathbb{C}} = \mathbb{C}\cup \{\infty\}$ with the extended arithmetic

$\begin{aligned} z + \infty &= \infty\\ z \infty &= \infty\\ z/0 &= \infty\\ z/\infty &= 0 \end{aligned}$ for $z\in \mathbb{C}\setminus\{0\}$ . In this round about way, we may for example view $z\mapsto 1/z$ as a continuous function $\varphi:\overline{\mathbb{C}}\rightarrow \overline{\mathbb{C}}$ with $\varphi(0) = \infty$ and $\varphi(\infty) = 0$ .

1.4 Projective spaces

For a field $k$ we let $\mathbb{P}^n(k)$ denote the set of lines through $0$ in $k^{n+1}$ i.e.,

$\mathbb{P}^n(k) = \{[\alpha] \mid \alpha \in k^{n+1}\setminus \{0\}\},$ where $[\alpha] = \{ t \alpha \mid t\in k\}$ . Notice that $[\alpha] = [\beta]$ if and only of $\alpha = c \beta$ for $c\in k\setminus\{0\}$ . This in fact gives an equivalence relation $\sim$ on $k^{n+1}\setminus\{0\}$ and we may make the identification

$\mathbb{P}^n(k) = k^{n+1}\setminus\{0\}/_\sim$ and write

$[x_0, x_1, \dots, x_n] := [(x_0, x_1, \dots, x_n)].$

We let $\mathbb{P}^n(k)_{x_i}$ denote the subset

$\{[x_0, x_1, \dots, x_n] \mid x_i \neq 0\} \subset \mathbb{P}^n(k).$

Notice that we have bijective maps $\varphi_i: k^n\rightarrow \mathbb{P}^n(k)_{x_i}$ given by

$\varphi_i(x_1, \dots, x_n) = [x_1, \dots, x_{i-1}, 1, x_i, \dots, x_n].$ If $k^{n+1}\setminus\{0\}$ carries a topology, then $\mathbb{P}^n(k)$ can be equipped with the quotient topology.

$\mathbb{P}^n(\mathbb{C})$ is a compact topological space.

Use the surjective continuous map $\varphi: S^n_\mathbb{C}\rightarrow \mathbb{P}^n(\mathbb{C})$ given by

$\varphi(z_0, \dots, z_n) = [z_0, \dots, z_n],$ where

$S^n_\mathbb{C} = \{(z_0, z_1, \dots, z_n) \mid z_0 \overline{z}_0 + \cdots + z_n\overline{z}_n = 1\}.$ Here $S^n_{\mathbb{C}}$ is a closed and bounded subset of $\mathbb{C}^{n+1}\cong \mathbb{R}^{2n + 2}$ .

Why is projective space interesting? Because it is a remarkable abstraction of the Riemann sphere. In fact, we have

$\mathbb{P}^1(\mathbb{C})$ is homeomorphic to the Riemann sphere $\overline{\mathbb{C}}$ .

This is perhaps not such a big surprise, since $\mathbb{P}^1(\mathbb{C}) = \mathbb{C} \cup \{\infty\}$ , where $\infty = [(1,0)]$ .

Define a metric $d: \mathbb{P}^1(\mathbb{C})\times \mathbb{P}^1(\mathbb{C}) \rightarrow \mathbb{R}$ , which gives the topology on $\mathbb{P}^1(\mathbb{C})$ . Prove that the distance from $\infty = [(1, 0)]$ to $[(z, 1)]$ is

$\frac{2}{\sqrt{1 + x^2 + y^2}},$ where $z = x + i y$ . In particular, $d(0, \infty) = 2$ .

A polynomial $f\in k[x, y, z]$ is called homogeneous if all its terms have the same degree.

$x^2 + y^2 - 1$ is not a homogeneous polynomial, since it has terms of degree zero and two, whereas $x^2 + y^2 - z^2$ is a homogeneous polynomial in $k[x, y, z]$ with each term of degree two.

Let $F = x^2 + y^2 - z^2\in \mathbb{C}[x, y, z]$ and $f = x^2 + y^2 - 1 \in \mathbb{C}[x, y]$ .

Consider $\mathbb{C}^2$ as an open subset of $\mathbb{P}^2(\mathbb{C})$ using the injective map $\varphi:\mathbb{C}^2\rightarrow \mathbb{P}^2(\mathbb{C})$ given by

$\varphi(x, y) = [x, y, 1]\in \mathbb{P}^2(\mathbb{C})_{x_2}$

By abuse of notation, we let $V(f)$ denote $\varphi(V(f))\subset \mathbb{P}^2(\mathbb{C})$ .

Show that
$F(\lambda x, \lambda y, \lambda z) = \lambda^2 F(x, y, z)$ for $\lambda \in \mathbb{C}$ .
Explain why
$V(F) = \{[x, y, z] \mid F(x, y, z) = 0\}$ is a well defined subset of $\mathbb{P}^2(\mathbb{C})$ .
Show that $V(F)$ is a closed subset of $\mathbb{P}^2(\mathbb{C})$ .
$V(F) \setminus V(f)$ consists of only two points! Find them.
Prove that $V(F) = \overline{V(f)}$ in $\mathbb{P}^2(\mathbb{C})$ .