9Convex optimization
In this last chapter we will deal exclusively with convex optimization problems.Recall that a convex optimization problem has the form where is a convex subset (see Definition 4.18) and a convex function (see Definition 4.23). We will mainly deal with the case, where is differentiable defined on all of in addition to just being convex defined on . Also recall that convex optimization problems are very well behaved in the sense that local minima are global (see Theorem 6.12).
Below is an example of a convex optimization problem in the plane .
where is the subset of points in satisfying
Sketch the subset in Example 9.1. Show that Example 9.1 really is a
convex optimization problem and solve it.
Below is an example of a convex optimization problem modelling the real life problem of placing a fire station (center of circle) so that the maximal distance to the surrounding houses (points to be enclosed) is minimal.
Given points
, what is the center and
radius of the smallest circle containing these points?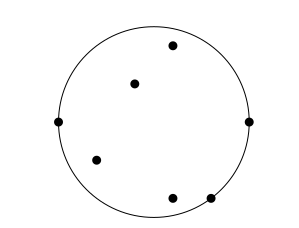 We can write this optimization problem as
where
Upon rewriting this turns into the optimization problem
where
and .
We can write this optimization problem as
where
Upon rewriting this turns into the optimization problem
where
and .

Prove that (9.1) and (9.2) both are convex optimization problems.
Explain how (9.1) is rewritten into (9.2).Hint
Expand
and put .
9.1 Finding the best hyperplane separating data
In section 5.2.3 we were presented with labeled data where and . The task at hand was to separate differently labeled data by a hyperplane , such that for . Please browse back to section 4.6 for the definition of a hyperplane in .To make this more real, consider the points with label and the points with label . Here a hyperplane satisfying (9.4) cannot exist: suppose that . Then (9.4) is tantamount to the following inequalities But these inequalities are unsolvable in and (why?).If the data in (9.3) can be separated according to (9.4), we may find a hyperplane , such that What does best hyperplane mean in this setting? This is the one maximizing the width of the strip between the two labeled clusters.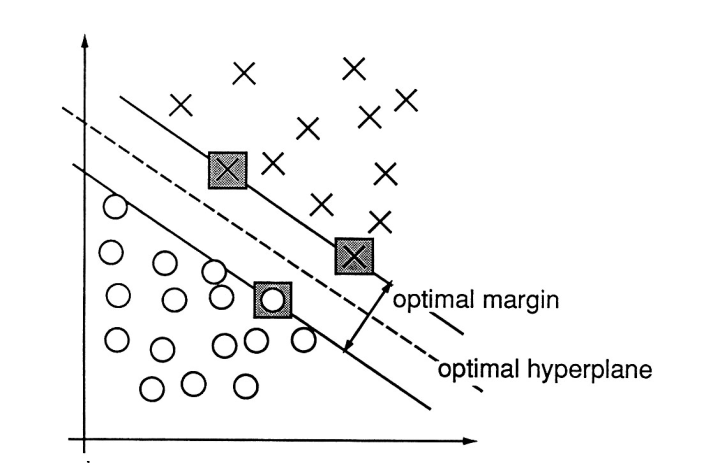
Let be the hyperplane in given by and let .
The point closest to in can be found by solving the optimization problem
Explain why (9.6) is a convex optimization problem.Show how Theorem 7.37 can be used to solve this optimization problem by
first deducing the equations
for the Lagrange multiplier . Notice here that
above really contains equations, whereas
is only one equation in , where
. Solve the equations (9.7) for and .
How can we be sure that really is a minimum in
(9.6)?Finally show that the distance from to is given by the formula
The optimal hyperplane is therefore (maximizing is the same as minimizing )
found by solving the convex optimization problem
Let us explicitly write up the optimization problem (9.8) in
a very simple situation: finding the best line separating the points
and . In the notation of (9.5), we have (without the
stars on and )
so that
The points are
where and .Therefore (9.8) takes the form
Solve the optimization problem (9.9) and verify that the best line
from the optimization problem is the one we expect it to be. Also, check how
WolframAlpha solves this optimization problem.Hint
Notice that (9.8) has number of constraints equal to the
number of points to be separated. For an extended (soft margin)
optimization problem, when the data at hand cannot be separated we
refer to section 3 of the
Cortes and Vapnik paper.
Usually one does not use the optimization problem formulated in (9.8), but
rather its socalled (Lagrange) dual for finding the optimal hyperplane. This dual
optimization problem uses that is a linear combination
of the support vectors. It is an optimization problem
in
from (9.10) and looks like
where is the vector of labels attached to
the points and is the symmetric
matrix given by
The dual optimization problem (9.11) can be derived
formally from the original optimization problem
(9.8). This is, however, beyond the scope of this
course (see section 2.1 of the Cortes and Vapnik paper).
You could maybe use Fourier-Motzkin elimination to show that
implies .
Quadratic optimization problems, such as (9.8) can in fact be handled by Sage (well, python
in this case). See
CVXOPT for
further information. Note that the code below needs to be
executed as Python code (choose Python in the pull
down). It attempts (in general) to solve the optimization
problemIn the Sage window below the optimization problem
has been entered.What happens if you remove
RealNumber=float
Integer=int
Take a look at the input format in Example 9.10. Can you tell which
optimization problem in this chapter is solved below? Also, the code below seems to report some errors after pressing the compute button. Can you make it run smoothly by making a very, very
small change?
9.1.1 Separating by non-linear functions
Sometimes one needs more complex separating curves than just a line. Consider the five points where we wish to separate from the other points. This is impossible using a line, but certainly doable by a circle where :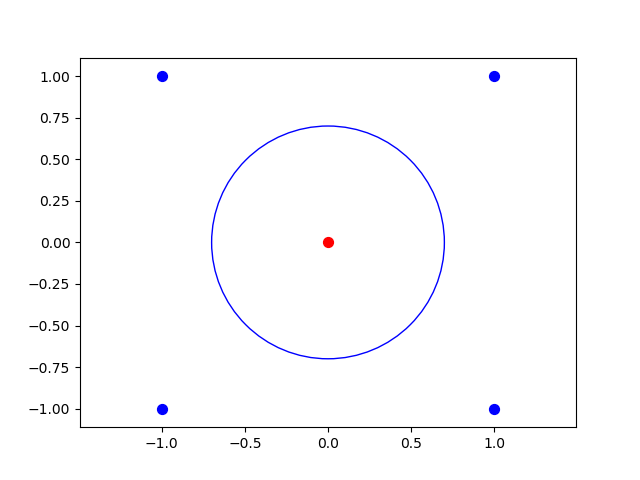
9.1.2 Kernels
A kernel is a function , that is a hidden dot product in the following sense: there exists a function such that
Let be given by
Then
One gleans from (9.16) that is a kernel function, since (9.15) is
satisfied for given by
The simplest example of non-linear separation comes from the one dimensional case :
consider the labeled points . Show by a drawing
that these points cannot be separated in , but that they become separable
in by using i.e., that the labeled points
are linearly separable
in .How does one glean from (9.16) that is a kernel function?
Once we have a kernel for we can replace the matrix in (9.14) byand proceed to solve the optimization problem without worrying about (or even an
infinite dimensional space).9.1.3 The kernel perceptron algorithm
Recall the stunningly simple perceptron algorithm from section 5.2.3. This algorithm can be modified to handle non-linear separation too by using kernel functions. In fact, this modification was one of the inspirations for the development of the support vector machines described above.After having mapped a set of vectors with labels to , via , we are looking for a vector , such that Such a vector is expressible as The (dual) perceptron algorithm works adjusting the coefficients successively as follows: if is wrong about the placement of in (9.17) i.e., if , then let If we have a kernel function for , then and we can use the kernel function in the algorithm without resorting to computing and the inner product in .
Use the kernel function in Example 9.12 and the kernel perceptron algorithm to
separate
Sketch the points and the separating curve.
9.2 Logarithmic barrier functions
We need an algorithm for solving optimization problems like (9.8). There is a very nice trick (probably going back to von Neumann) for solving constrained optimization problems of the form where is defined by the differentiable functions as The functions define the boundary (or barrier) of . We use them to define the logarithmic barrier function defined on the interior The boundary of is You can see that the logarithmic barrier function explodes (becomes unbounded), when a vector approaches , since is unbounded as for .The cool idea is to consider the function for . This function has a global minimum .
Prove that is a convex function if and are
convex functions.Hint
The upshot is that as . This is the content of the following theorem, which we will not prove.
Prove and use that if is a decreasing convex function (in one variable) and is a convex function, then
is a convex function, where we assume the composition makes sense.
Let be a point in with
for and . Then
and as . If
(9.18) has a unique optimum ,
then by using we obtain a sequence as .
9.2.1 Quadratic function with polyhedral constraints
A much used setup in optimization is minimizing a quadratic functions subject to polyhedral constraints. This is the optimization problem where is an matrix, is an matrix, and .Certainly the constraints define a convex subset of , but the function is not strictly convex unless is positive definite. If is not positive semidefinite (9.20) is difficult.If is positive semidefinite, the interior point method outlined above usually works well.
The optimization problem (9.8) has the form (9.20), when we put
Here is a matrix, is an matrix and
.
Optimization of a quadratic function as in (9.20) is implemented below using the
interior point method and exact line search. See Section 10.5.1 of my book Undergraduate Convexity for further details. Only
python with numpy is used. Below are samples of output running the interior point algorithm on the enclosing circle problem in Example 9.3.
in the barrier function in (9.19). We are attempting to compute the center
of the smallest enclosing circle of the points
>>> Newton(Q1, c1, A1, b1, [0,0,18], 1)
array([-0.43814179, 1.84835643, 7.69779763])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.5)
array([-0.45244596, 1.81135335, 4.99353576])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.1)
array([-0.49569549, 1.84020923, 2.91071666])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.05)
array([-0.49875614, 1.87002433, 2.63917096])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.01)
array([-0.4999099 , 1.93327221, 2.28805064])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.005)
array([-0.49996901, 1.95176304, 2.20331123])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.001)
array([-0.49999729, 1.97792915, 2.09031159])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.0005)
array([-0.49999904, 1.98432672, 2.06370265])
>>> Newton(Q1, c1, A1, b1, [0,0,18], 0.0001)
array([-0.49999991, 1.99295433, 2.0283835 ])
Try out the code in the Sage window above on the Exercises 7.48, 7.49 and
7.50. Check the output of the code by actually solving these exercises.
Compute the best line separating the labeled data
((1, 0), +1), ((2, 0), +1), ((3, 0), +1), ((3, 2), +1), ((1, 1), -1), ((2, 2), -1).
9.3 A geometric optimality criterion
Consider the general optimization problem where is a subset of .
Proof
If is an optimal solution and , then
for every with , where denotes the
epsilon function in the definition of differentiability (see
Definition 7.5). Therefore
for . This is only possible if . We have silently applied the convexity of
and the differentiability of at .If in addition is convex and (9.22) holds, then
Theorem 8.19 shows that is an optimal solution.
A nice application of Proposition 9.22 is for example to the optimization problemHere Proposition 9.22 shows that is optimal, since
the hyperplane
touches the boundary of
as shown below.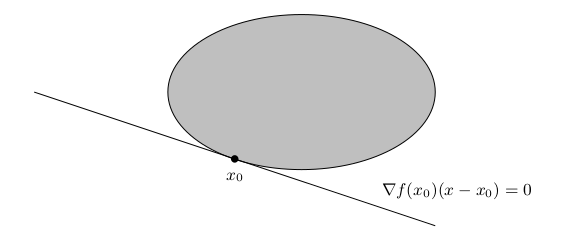

Sketch how Proposition 9.22 applies to show that an optimum in a linear programming
problem
in the plane always can be found in a vertex.
Let be a differentiable convex function and
Suppose that for . Prove that is a minimum for defined on
.
Guess the solution to the optimization problem
Show that your guess was correct!
9.4 KKT
The KKT in the title of this section is short for Karush-Kuhn-Tucker.We will limit ourselves to a convex optimization problem of the form where is defined by the differentiable convex functions for as and is a convex function.To the optimization problem (9.23) we associate the (famous) Karush-Kuhn-Tucker (KKT) conditions:Notice that the KKT conditions consist of inequalities and
equations in the unknowns
. The KKT
conditions form a surprising theoretical foundation for optimization
problems of the type in (9.23). You should take a peek back
to the theory of Lagrange multipliers in section 7.9 and
compare with (9.24).
The KKT conditions associated with the convex optimization problem in (9.1) are
Verify that the KKT conditions of the optimization problem in (9.1) are the
ones given in Example 9.27.
To state our main theorem we
need a definition.
The optimization problem (9.23) is called strictly
feasible if there exists with
Let us now touch base with a rather simple example. Consider the optimization problemHere and in (9.23). Therefore
the KKT conditions in (9.24) are
Before even thinking about moving on to the next section, you should attempt to
find a solution to the above KKT conditions (inequalities) and then verify using Theorem 9.30(ⅱ.) that is optimal. Also, try only using Theorem 9.30(ⅰ.) and (9.26) to show that is not
a solution to (9.25).
Give an example of a convex optimization problem as in (9.23), which is not strictly feasible and with an optimal solution that does
not satisfy the KKT conditions. Such an example shows that strict feasibility is necessary in Theorem 9.30(ⅰ.).
9.5 Computing with KKT
9.5.1 Strategy
A general strategy for finding solutions to the KKT conditions in (9.24) is zooming in on (the Lagrange multipliers) testing each of them for the two cases and .One important point, which you can read from (9.24), is that if . To further elaborate, if , then an optimal solution must satisfy .
So where exactly in (9.24) is the above claim verified?
The condition simplifies the equations
in (9.24). In principle to solve the KKT conditions, one has to try out all the
possibilities coming from or for .
Why possibilities above?
How do you solve the optimization problem (or decide there is no solution)
if ?
9.5.2 Example
Let denote the set (see Figure 9.35) of points with We will illustrate the mechanics of solving the KKT conditions in finding an optimal solution for
9.6 Optimization exercises
Below are some exercises especially related to the KKT conditions. In some of the exercises the minimization problem is denoted This should cause no confusion. Consider the optimization problem
- Show that (9.29) is a convex optimization problem.
- Sketch the set of constraints in and show that cannot be an optimal solution to (9.29).
- Write up the KKT conditions for (9.29) and explain theoretically (without actually solving them) why they must have a solution.
- Now solve (9.29). Is the solution unique?
Consider the function given by
- Show that is strictly convex.
- Let denote the subset of points satisfying Show that is a closed convex subset.
- Solve the optimization problem
Let , where
- Why does the optimization problem have a solution?
- Find all optimal solutions to (9.31).
- Let , where at least one of is non-zero. Show that an optimal solution to belongs to .
Let
- Use the KKT conditions to solve the minimization problem
- Use the KKT conditions to solve the minimization problem
Solve the optimization problem
Let
and .
- State the KKT conditions for for .
- Suppose now that . For which and does have optimum in ? State the KKT conditions when .
Let be given by
- Show that is a convex function.
- Find . Is this minimum unique? Is a strictly convex function.Let
- Apply the KKT-conditions to decide if is an optimal solution to
- Find and
Let be given by
and let
- Show that is not a convex function.
- Show that is a convex function on the open subset and conclude that is convex on .
- Show that is an optimal solution for the optimization problem . Is a unique optimal solution here?
Let be given by
and by
- Show that is a convex function. Is strictly convex?
- Show that is a convex subset of .
- Does there exist an optimal point for the minimization problem with ?
- Does there exist an optimal point for the minimization problem with ?
Let
and
Solve the optimization problem
Let be given by
Below, the minimization problem
is analyzed for various subsets .
Let be given by
- Show that is a convex function and solve the minimization problem .Now let and consider the minimization problem (P) given by
- Show using the KKT conditions that is not optimal for (P).
- Find an optimal solution for (P). Is it unique?